Интуитивная математика Месопотамии

Разглядывая в музеях фрагменты керамики доисторических мастеров, вы вряд ли стараетесь найти какую-то систему в наборах линий или пятнышек сохранившейся краски. Фрагмент из книги Микаэля Лонэ «Большой роман о математике» расскажет о том, как неожиданно смотрит на древнее искусство математик.
Вдоль Плодородного полумесяца, на территории современного Ирака, десять тысяч лет назад происходил революционный переход к неолиту... В северных районах люди переходили к оседлому образу жизни. В этом регионе возникали все наиболее продвинутые достижения человечества. Жилища из необожженной глины формировали первые поселения, а самые смелые строители уже возводили дополнительные этажи... Совсем скоро будет открыто гончарное ремесло.
...В Лувре меня окружают доверху заполненные стеллажи. Самые ранние экспонаты датируются 9000 г. до н. э., и из зала в зал, словно следуя по камушкам, оставленным Мальчиком-с-пальчик, мы попадаем из одного века в другой. В витринах представлена посуда самых разных размеров, форм, по-разному украшенная, вылепленная, покрашенная или гравированная, на ножках и с ручками, в идеальном состоянии и с трещинами, разбитая и воссозданная. От некоторых вещей остались лишь небольшие фрагменты.
Керамика — это первое искусство с применением огня, появившееся раньше, чем технологии изготовления бронзы, стали и стекла. ...Прогуливаясь по залам кафедры восточных древностей, я был поражен богатством геометрических узоров, разработанных в Месопотамии…
Я рассматриваю их один за другим, и во мне просыпается математик. Я обращаю внимание на симметрию, изгибы, геометрические узоры. Так, я невольно начинаю сортировать и упорядочивать их. Мне вспоминаются несколько теорем из моей юности. Классификация геометрических преобразований — это то, что я собирался сделать. Я достаю блокнот и карандаш и начинаю записывать…
Сколько же всего типов узоров я найду? Немного поразмыслив, наконец останавливаюсь на известной теореме. Можно выделить всего семь типов узоров, семь групп — ни больше, ни меньше. Конечно же, жители Месопотамии не знали этого. Теоретическое осмысление, без сомнения, началось только в эпоху Ренессанса. Тем не менее, не претендуя на что-то большее, чем просто украшение керамики, горшечники древности были на пороге первых открытий, которые тысячи лет спустя станут волновать умы всего математического сообщества…
За тысячу лет до изобретения письменности гончары Месопотамии уже, сами того не осознавая, использовали все варианты теоремы, которая будет доказана лишь спустя шесть тысяч лет.
Как распознать семь типов узоров?
Первый тип — это узор, у которого нет какой-либо геометрической особенности. Просто обычный повторяющийся мотив без симметрии или центра вращения. Это пример узора, не основанного на геометрических фигурах, в изображении которого используются изображения фигур, например животных.
Второй тип — это узор с горизонтальной осью симметрии посередине.
Третий тип узора включает в себя повторяющиеся по горизонтали элементы с осью симметрии по вертикали. В таком узоре элементы повторяются по горизонтали, каждый из данных элементов имеет оси симметрии по вертикали.
Четвертая категория — это орнаменты, которые выглядят одинаково при развороте на 180°. Такие узоры не меняются, если на них смотреть сверху или снизу.
Пятый тип узоров построен на скользящей симметрии. Это тот самый знаменитый узор, который мне посчастливилось найти среди экспонатов из Месопотамии. Если вы развернете один из таких узоров по горизонтали (как во втором случае), то получится та же картинка, только сдвинутая на пол-элемента.
Шестой и седьмой типы орнаментов не являются какими-то новыми относительно пяти первых и сочетают в себе их особенности в различных вариациях. Так, шестой тип включает горизонтальную и вертикальную симметрию, а также центр вращения на пол-оборота.
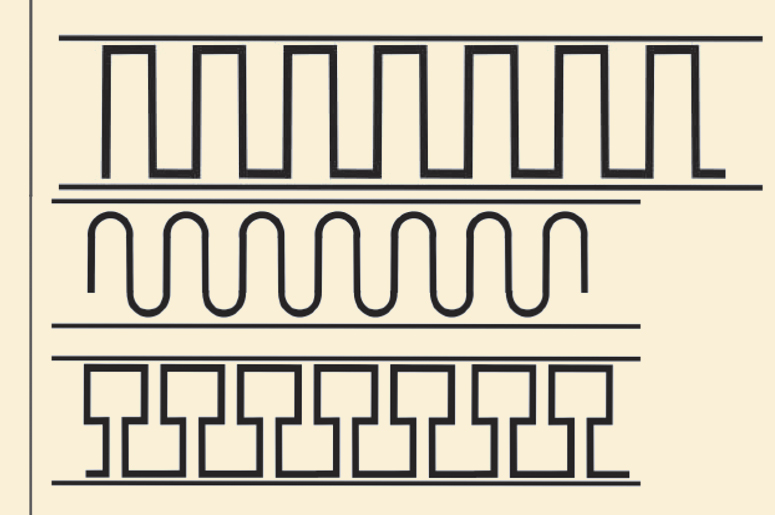
Ну а седьмая категория сочетает узоры с вертикальной симметрией, центр вращения и скользящую симметрию. Следует отметить, что эти категории относятся только к геометрическим особенностям и не ограничивают вариативность конкретных узоров. Так, узоры, изображенные далее, хотя и отличаются визуально, все относятся к последней, седьмой категории.
Все узоры, которые только возможно представить, можно отнести к одной из семи категорий. Создать иные узоры, с геометрической точки зрения, невозможно. Удивительно, но последние две категории наиболее распространены. Человеку интуитивно свойственно использовать узоры с большим количеством типов симметрии.
Этого достаточно, чтобы изменить свой взгляд на мир, чтобы констатировать существование в повседневности математики. Ее проявления можно искать бесконечно, и этот поиск невероятно увлекателен.
«Математика — это сложно». Не правда ли, мы слышим это постоянно, да и сами порой так думаем. Неужели математика это обязательно что-то сложное и пугающее? Почему само это слово внушает страх? Математику не любят, но хотят заглянуть в замочную скважину ее непостижимых тайн.
Каково прошлое математики, на что будет похожа математика будущего? Никто не знает, что еще смогут открыть ученые, но точно можно сказать, что нас ждет множество сюрпризов, исследований и открытий. Прочитав книгу Микаэля Лоне «Большой роман о математике», вы поверите в то, что заниматься математикой совсем не сложно.
Издательство: «Эксмо»