Значимые фигуры

История Мухаммада аль-Хорезми — одного из великих математиков Средневековья, когда Восток был мировым центром научной деятельности. Фрагмент из книги Иэна Стюарта «Значимые фигуры», описывающей судьбы 25 величайших математиков в истории — от Архимеда до Уильяма Тёрстона.
Мухаммад аль-Хорезми
Примерно в 800 г. Гарун аль-Рашид основал «Байт аль-хикма», или «Дом мудрости», — академию, в которой письменные труды из других культур переводились на арабский язык. Его сын аль-Мамун довел проект отца до логического завершения — собрал в Байт аль-хикма огромную коллекцию греческих рукописей и пригласил многих известных ученых. Багдад, ставший центром науки и торговли, привлекал купцов и ученых мужей даже из таких отдаленных мест, как Китай и Индия. Среди них был и Мухаммад ибн Мусса аль-Хорезми — ключевая фигура в истории математики.

Аль-Хорезми родился в Хорезме или где-то неподалеку от него; Хорезм — это город в Средней Азии, современная Хива в Узбекистане (Неточность автора, Хорезмом в разное время называли регион или государство — Прим. ред.). Главные работы аль-Хорезми относятся ко времени правления аль-Мамуна; он участвовал в сохранении и развитии тех знаний, которые тогда стремительно теряла Европа. Он переводил ключевые рукописи с греческого и санскрита, делал собственные открытия в физике, математике, астрономии и географии и написал серию книг, которые мы сегодня назвали бы научными бестселлерами. Название книги «Об индийском счете», написанной около 825 г., было переведено на латынь как Algoritmi de Numero Indorum; в то время это был практически единственный трактат, распространявший по всей Европе новость о поразительном способе проведения арифметических расчетов. По пути Algoritmi превратились в Algorismi, и методы расчета с применением десятичных чисел получили название алгоризмов. В XVIII в. это слово изменилось и приобрело сегодняшнюю форму — алгоритм.
Отец алгебры на самом деле не делал ничего из того, что сегодня большинство из нас считает алгеброй. Он все описывал словами
Его книгу «Аль-китаб аль-мухтасар фи хисаб аль-джебр ва-ль-мукабала» («Краткая книга об исчислении алгебры и аль-мукабалы»), написанную около 830 г., Роберт Честерский в XII в. перевел на латынь с названием Liber Algebrae et Almucabola. В результате аль-джебр, латинизированное до algebra, стало самостоятельным словом. Теперь оно означает использование таких символов, как x и y, для неизвестных величин, а также методы отыскания этих неизвестных путем решения уравнений, но в самой книге никакие символы не используются.
«Алгебра» была написана, когда халиф аль-Мамун предложил аль-Хорезми написать популярную книгу о вычислениях. Сам автор описывает ее цель так: «…здесь содержится простейшее и полезнейшее в арифметике, постоянно необходимое людям в случаях наследования, завещаний, раздела имущества, судебных тяжб и торговли и в любых сделках друг с другом или когда речь идет об измерении земель, рытье каналов, геометрических расчетах и других вещей разных сортов и типов».
Все это не слишком похоже на книгу по алгебре. И правда, непосредственно алгебра занимает в ней лишь небольшую часть. Аль-Хорезми начинает с объяснения чисел в очень простых выражениях — единицы, десятки, сотни — на том основании, что «когда я думаю о том, в чем люди обычно нуждаются при расчетах, я понимаю, что это всегда число». Вообще, это не ученый трактат для мужей науки, но популярная математическая книга, практически учебник, который пытается не только информировать, но и обучать обычных читателей. Именно этого хотел халиф, и именно это он получил. Аль-Хорезми не рассматривал свою книгу как результат работы на переднем крае исследовательской математики. Но мы сегодня именно так смотрим на ту ее часть, которая посвящена аль-джебре. Это самый глубокий раздел книги: систематическое развитие методов решения уравнений с некоторой неизвестной величиной.
Аль-Хорезми... приводит универсальные методы решения, тогда как его предшественники, как правило, брали пример с конкретными числами и решали его
Собственно термин «аль-джебр», который обычно переводят как «дополнение», относится к приему добавления одного и того же слагаемого к обеим частям уравнения с целью его упрощения. «Аль-мукабала», или «уравновешивание», относится к переносу одного из слагаемых с одной стороны уравнения на другую сторону (но с противоположным знаком) и к сокращению подобных членов в обеих частях уравнения…
Отец алгебры на самом деле не делал ничего из того, что сегодня большинство из нас считает алгеброй. Он все описывал словами. Конкретные числа были единицами, неизвестная величина, которую мы называем x, называлась у него корнем, а наш x2 назывался квадратом… Уравнение в этих терминах выглядело бы так: квадрат плюс корень равно двенадцать единиц, и без всяких символов. Так что следующая задача — объяснить, как от уравнения подобного типа перейти к ответу. Аль-Хорезми подразделяет уравнения на шесть типов, причем типичный случай представляет собой «квадраты и корни равняются числам», то есть что-то вроде x2 + x = 12. Затем он переходит к анализу каждого типа уравнений по очереди, причем решает их с использованием смеси алгебраических и геометрических методов.
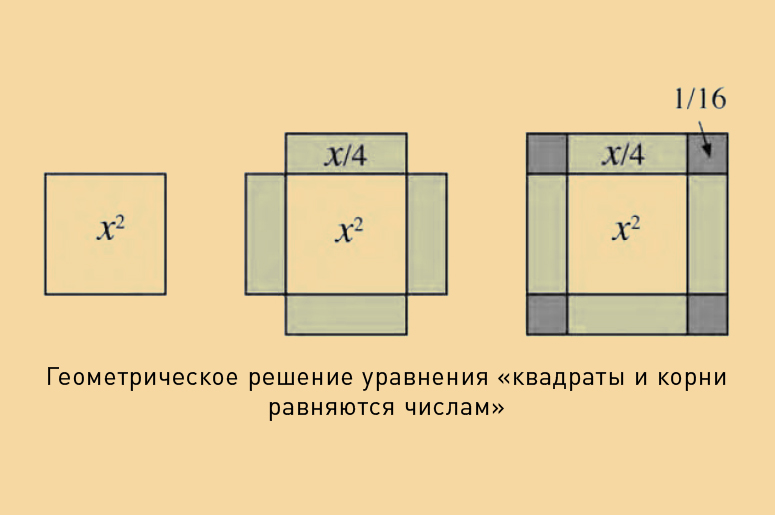
Такой подход был бы понятен и вавилонянам, и грекам, поскольку они и сами в свое время занимались примерно тем же. На самом деле существуют сомнения относительно того, был ли аль-Хорезми знаком с «Началами» Евклида. По идее, должен был быть знаком, поскольку аль-Хаджжадж — другой ученый из «Дома мудрости» — перевел Евклида на арабский, когда аль-Хорезми был молодым человеком. Но с другой стороны, основной задачей «Дома мудрости» был именно перевод, и его работники не были обязаны читать труды, переведенные их коллегами. Некоторые историки утверждают, что геометрия аль-Хорезми по стилю не соответствует Евклидовой, и это свидетельствует о том, что ученый не был знаком с оригиналом. Но, я повторяю, «Алгебра» — популярная книга о математике, так что она и не должна была бы следовать аксиоматическому стилю Евклида, даже если бы сам аль-Хорезми знал Евклида назубок. Во всяком случае, идея достраивания квадрата восходит еще к вавилонянам и позаимствовать ее можно было из множества разных источников.
Важнейшим трудом аль-Хорезми как на момент написания, так и на протяжении еще нескольких столетий была «Книга об индийском счете», давшая нам... слово «алгоритм»
Почему же тогда многие историки считают именно аль-Хорезми отцом алгебры? Особенно с учетом того, что он не использует никаких символов? И у него имеется сильный конкурент, грек Диофант. В его «Арифметике» — серии книг о решении уравнений в натуральных или рациональных числах, написанной около 250 г., — символы используются. Один из ответов состоит в том, что главной областью интересов Диофанта была теория чисел, да и символы его были, по существу, простыми сокращениями. Однако более глубокий ответ, который мне кажется и более убедительным, заключается в том, что аль-Хорезми часто, хотя и не всегда, приводит универсальные методы решения, тогда как его предшественники, как правило, брали пример с конкретными числами и решали его. Читателю оставалось самому выводить общее правило…

Важнейшим трудом аль-Хорезми как на момент написания, так и на протяжении еще нескольких столетий была «Книга об индийском счете», давшая нам, как уже отмечалось, слово «алгоритм». Фраза Dixit Algorismi — «Так говорил аль-Хорезми» — была весьма убедительным аргументом в любом математическом диспуте. Учитель сказал: внимайте его словам.
Под индийским счетом подразумеваются, безусловно, ранние варианты десятичной системы записи чисел, в которой любое число может быть записано как последовательность десяти символов — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Как видно из названия книги, аль-Хорезми признавал первенство индийских математиков в этом вопросе, но его влияние в средневековой Европе было настолько велико, что такую систему исчисления стали называть арабской (иногда ее называли еще индо-арабской системой, что тоже несправедливо по отношению к индусам). Основной вклад арабского мира в эту систему — изобретение собственных символов для обозначения цифр, похожих на индийские, но все же отличных от них, а также распространение этой системы записи и побуждение к ее использованию. Символы же для обозначения десяти цифр не раз менялись с течением времени, и разные регионы современного мира до сих пор пользуются разными их вариантами...

Наряду с достижениями математиков древнего Китая и Индии достижения аль-Хорезми служат дополнительным свидетельством того, что в Средние века, когда наука Европы в основном находилась в состоянии застоя, центр научной и математической деятельности переместился на Восток. Со временем, в эпоху Возрождения, Европа пробудилась вновь... Аль-Хорезми проложил новый путь, и математике уже не суждено было вернуться в прежнее состояние.
Несмотря на загадочное происхождение отдельных своих элементов, математика не рождается в вакууме: ее создают люди. Некоторые из этих людей демонстрируют поразительную оригинальность и ясность ума. Именно им мы обязаны великими прорывными открытиями, именно их называем пионерами, первопроходцами, значимыми фигурами математики. Иэн Стюарт в книге «Значимые фигуры» описывает открытия и раскрывает перед нами судьбы 25 величайших математиков в истории — от Архимеда до Уильяма Тёрстона.
Издательство: «Альпина»




















