Математики разгадали парадокс развязывания узлов спустя 88 лет

Почему два узла могут быть легче для распутывания, чем один? Ответ на этот вопрос озадачил математиков почти на столетие. Теперь команда из Университета Небраски в Линкольне доказала: объединение двух сложных узлов может быть проще для распутывания — вопреки интуиции и 88-летней гипотезе. Результаты были размещены на сервере препринтов arXiv.
«Мы искали контрпример, не особо рассчитывая на его нахождение», — признается один из авторов открытия, профессор Марк Бриттенхэм. — «Это было очень неожиданно и удивительно».
Что такое теория узлов?
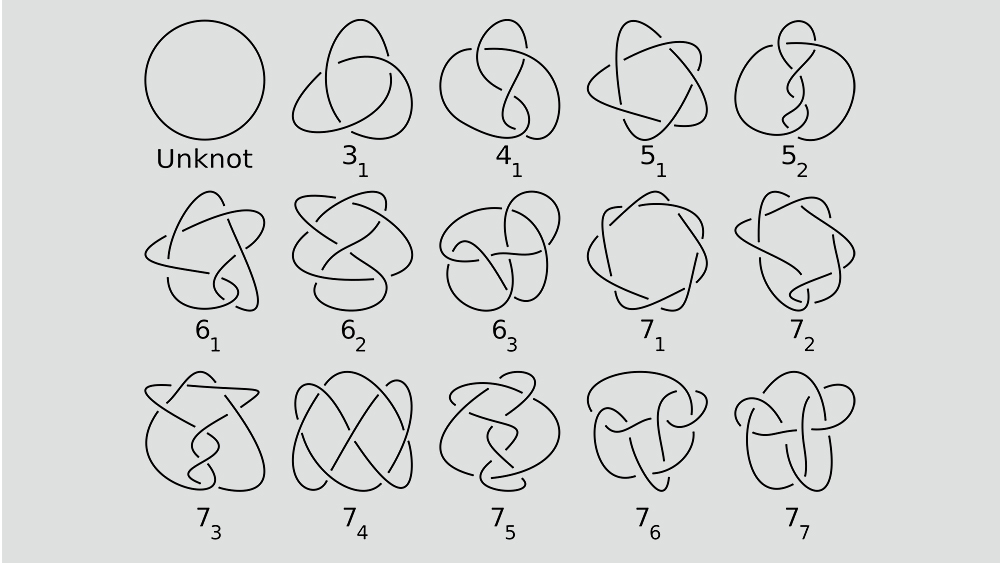
Теория узлов — это раздел математики, который изучает петли с соединёнными концами, как если бы вы завязали шнурок, а потом спаяли его концы вместе. Ключевое понятие здесь — число распутывания: сколько раз теоретически нужно «разрезать», переставить и «сшить» петлю, чтобы получить обычное кольцо без пересечений.
Сложные узлы состоят из более простых. Те, что нельзя разобрать дальше, называются простыми узлами — по аналогии с простыми числами.
В чем была загадка?
В 1937 году математики предположили, что если соединить два узла, то число распутывания объединенного узла будет равно сумме чисел распутывания его частей или больше. Иначе говоря, распутать составной узел должно быть как минимум так же трудно, как оба по отдельности.
Теперь Марк Бриттенхэм и его коллега Сьюзен Хермиллер показали, что это не всегда так. Они нашли не только один контрпример, но бесконечное множество таких случаев.
«Сначала мы нашли один, а потом — целую серию пар узлов, у которых число распутывания сложного узла оказалось меньше суммы частей», — рассказывает Хермиллер.
Простой эксперимент все показал

Хотя для поиска нужных узлов использовались математические методы, интуиция и вычисления, финальное подтверждение оказалось неожиданно простым: узлы завязали из обычной веревки и физически распутали, подтвердив теоретический расчет.
«Возможно, даже те узлы, которые не состоят из нескольких частей, можно распутать более эффективно, чем мы думали», — говорит Бриттенхэм. «Это открывает новые направления для исследований».
Почему это важно?
Теория узлов имеет практическое значение — от криптографии до изучения ДНК. Однако не все уверены, что новое открытие даст немедленные применения.
«Полагаю, мы просто стали немного лучше понимать, как работают окружности в трех измерениях», — сдержанно отмечает Николас Джексон из Университета Уорика.
Андраш Юхас из Оксфорда, который ранее пытался решить эту задачу с помощью искусственного интеллекта, подтверждает, насколько трудным был поиск:
«Мы сдались после пары лет безуспешных попыток. Видимо, ИИ — не лучший инструмент для таких задач».
Тем не менее, математическое сообщество признало прорыв. 88-летняя гипотеза оказалась ложной, и теперь у науки — новая, более полная картина того, как можно распутывать даже самые запутанные узлы.