Сколько лотерейных билетов нужно купить, чтобы гарантировать выигрыш? Математики нашли ответ

Ученые из Университета Манчестера анализировали вероятность выигрыша в самой популярной национальной лотерее Великобритании «Лото». В ней разыгрываются шесть случайных чисел от 1 до 59. Д-р Дэвид Стюарт и д-р Дэвид Кушинг обнаружили, что 27 — это наименьшее возможное количество билетов, необходимое для гарантированного выигрыша, хотя, что важно, без гарантии прибыли.

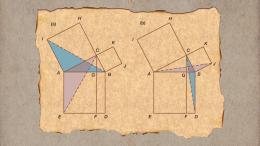
Они описывают решение, используя математическую систему, называемую конечной геометрией, которая в данном случае сосредоточена вокруг треугольной структуры — плоскости Фано. Каждая точка структуры — пара чисел, точки соединены линиями — каждая линия дает набор из шести чисел, что соответствует одному билету. Требуется три плоскости Фано и два треугольника, чтобы покрыть все 59 чисел и получить 27 наборов билетов.

Выбор билетов таким образом гарантирует, что независимо от того, какой из 45 057 474 возможных розыгрышей произойдет, по крайней мере в одном из 27 билетов будет как минимум два совпадающих номера: в любом розыгрыше шести чисел два числа должны появиться на одной из пяти геометрических структур, что гарантирует их появление хотя бы в одном билете. Но добиться того же результата с 26 билетами невозможно.

Несмотря на гарантированный выигрыш, исследователи говорят, что шансы на получение прибыли очень малы и не должны использоваться в качестве причины для игры!

27 лотерейных билетов обойдутся в 54 фунта стерлингов. И почти в 99% случаев вы не вернете эти деньги — сумма выигрыша будет слишком маленькой. То есть открытие интересно исключительно с вычислительной точки зрения.