Физик и его домашний питомец вывели уравнение движения кошки

В эпоху социальных сетей нет сомнения, кто является звездой животного царства. Благодаря Эрвину Шредингеру, кошки заняли почетное место в истории физики. Именно кошка по имени Эме вдохновила Анксо Биази, исследователя из Галисийского института физики высоких энергий (Испания), на публикацию статьи в American Journal of Physics. В статье Анксо предлагает уравнение движения кошки.

«Эта работа направлена на то, чтобы приблизить физику к неспециалистам, предлагая милый пример, с помощью которого можно понять несколько концепций классической механики. Для этого строится уравнение, моделирующее поведение кошки в присутствии человека, при этом кошка рассматривается как точечная частица, движущаяся в потенциале, создаваемом человеком», — объясняет он.

Потенциал — физическая величина, характеризующая энергию, напряжение и т. п. чего-нибудь в конкретной точке.

Анксо работает в области нелинейных эволюционных уравнений, на стыке физики и математики, в составе команды по теории струн и смежных областей. Идея этой статьи возникла для «веселого представления физики и привлечения студентов». То, что изначально казалось шуточной идеей, постепенно приобрело серьезную академическую форму.

Анксо использует семь паттернов (типов поведения кошки), выведенных из своего повседневного общения с Эме, и предполагает, что «кошки ведут себя так, будто ощущают силу вокруг человека». В статье утверждается, что указанные семь динамик можно смоделировать, рассматривая кошку как точечную частицу, подчиняющуюся законам Ньютона.

Кошка воспринимает «силу», связанную с внешним потенциалом, создаваемым присутствием человека, где x(t) представляет собой положение кошки во времени t относительно человека, находящегося в x = 0. Таким образом, m — это масса кошки, а ϵ — коэффициент трения, учитывающий усталость кошки. Результат — данное уравнение.

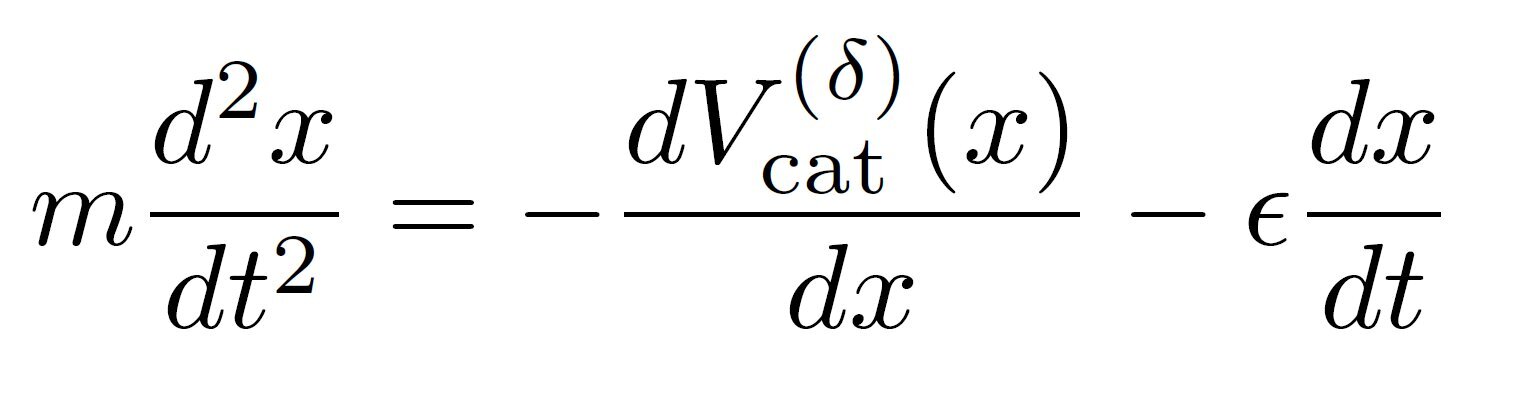
«Работа демонстрирует, в развлекательной форме, ментальный процесс построения физических моделей, который редко детализируется в книгах. Например, учитываются паттерны движения (или отсутствия движения), обусловленные тем, что кошки обычно не приходят на зов, легко отвлекаются или предпочитают оставаться на коленях у любимого человека».

Статья сосредоточена и на анализе мурлыканья кошки.

«Предполагается, что, когда кота гладят и он начинает мурлыкать, у людей возникает импульс продолжать гладить его, тем самым усиливая стабильность процесса. Эта стабилизация также подкрепляется тем, что обмен лаской между мурлыканьем и поглаживанием временно укрепляет связь между кошкой и человеком».

Также исследование учитывает периоды безумной активности, когда кошки мчатся на полном ходу из одной точки в другую, обычно ночью. В работе обсуждается, что в этом случае уравнение требует случайной компоненты для моделирования этих периодов, встроенной в формулу как внешнее усиление.

Анксо отмечает, что эта статья «предназначена для использования в вводных курсах по классической механике, чтобы показать, как внешне сложное и несвязанное поведение можно объяснить простыми законами. Она делает это, демонстрируя ряд динамик, которые легко визуализировать, сокращая необходимость в абстракции».