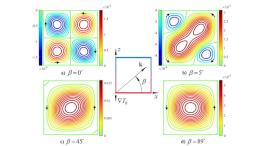
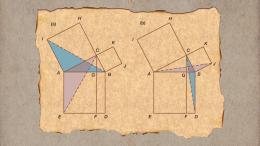
Ученые обнаружили красивую математическую закономерность в эволюционной генетике

«Красота теории чисел заключается не только в абстрактных соотношениях, но и в глубоких математических структурах, которые она раскрывает в мире природы», — объясняет математик из Оксфордского университета (Великобритания) Ард Луи, старший автор нового исследования, опубликованного в журнале The Royal Society Interface.
Луиса и его коллег интересовали мутации — генетические изменения, которые со временем возникают в геномах и приводят к эволюции. Некоторые мутации могут представлять собой изменение генетической последовательности, которое либо вызывает заболевание, либо дает какое-то неожиданное преимущество. Другие мутации не могут оказывать заметного влияния на внешний вид, черты или поведение организма (его фенотип).
Последние иногда называют нейтральными, и хотя они не имеют наблюдаемого эффекта, но являются индикаторами эволюции в действии. Мутации накапливаются с постоянной скоростью. Поскольку эта скорость известна, ученые могут сравнить процентную разницу в последовательности между двумя организмами и сделать вывод, когда жил их последний общий предок.
Однако организмы должны быть способны переносить некоторые мутации, чтобы сохранить свой характерный фенотип, в то время как генетическая лотерея продолжает раздавать «билеты», которые могут быть или не быть удачными. Эта так называемая мутационная устойчивость порождает генетическое разнообразие. Оно варьируется у разных видов и даже может наблюдаться в белках внутри клеток.
«Мы уже давно знаем, что многие биологические системы демонстрируют удивительно высокую устойчивость фенотипа, без которой эволюция была бы невозможна. Но мы не знали, какой будет абсолютная максимальная возможная надежность и существует ли вообще максимум», — объясняет Луис.
В рамках исследования ученые рассмотрели сворачивание белков и структуры малых РНК. Луис и его коллеги задавались вопросом, насколько близко природа может подойти к верхним границам мутационной устойчивости, поэтому провели численное моделирование. Они изучили математические особенности того, сколько генетических изменений может соответствовать определенному фенотипу, не изменяя его.
Максимальная устойчивость соответствовала самоповторяющемуся фрактальному образцу, называемому «кривой бланманже». Кроме того, она была пропорциональна базовому понятию теории чисел: дроби суммы цифр — логарифму доли всех возможных последовательностей, которые соответствуют фенотипу. Например, для n = 123 в десятичной системе счисления сумма цифр будет равна 1 + 2 + 3 = 6.
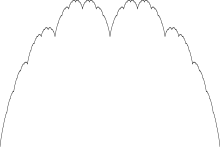
Первый автор доктор Вайбхав Моханти (Гарвардская медицинская школа) добавил: «Самым удивительным является то, что мы нашли четкие доказательства, что природа в некоторых случаях достигает точного предела максимальной устойчивости и не переходит его. Как будто биология знает о фрактальной функции суммы цифр».