Человек, который поставил планеты на место

Иоганн Кеплер был немецким математиком и астрономом, но не брезговал также составлением астрологических гороскопов и, как показывают недавние исследования, возможно, даже увлекался алхимией. Страсть к астрономии ему привила мать-трактирщица, которая подрабатывала гаданием и траволечением. В 1577 году она показала маленькому сыну большую яркую комету, а три года спустя — лунное затмение 1580 года. После этого Кеплер уже не мог забыть о тайных знамениях небес и, взрослея, стремился построить некую универсальную систему мироздания. Мистическая философия и строгая математика странным образом сочетались в его теории: мир он считал реализацией некоторой числовой гармонии, каковую оставалось лишь разгадать. Три закона, сформулированные им 400 лет назад, родились из интуиции и озарений, но в точности описали движения планет.
Тайна мироздания
Надо заметить, что астрономы конца XVI века еще не были уверены в том, как устроена Солнечная система, и разделялись на два лагеря: одни верили, что прав Птолемей и все планеты, Солнце, Луна и звезды вращаются вокруг неподвижной Земли. Другие же соглашались с Коперником и полагали, что именно Солнце является центром Вселенной, вокруг которого вращаются остальные небесные тела Солнечной системы. Около 1580 года датский астроном Тихо Браге выдвинул компромиссную версию: мол, все планеты, кроме Земли, вращаются вокруг Солнца, но Земля находится на особом положении — она неподвижно покоится в центре мира, заставляя крутиться вокруг себя Солнце и Луну. Так, геоцентрическая и гелиоцентрическая система мира объединились в гибридную геогелиоцентрическую. Но вопросы остались: как именно планеты вращаются, по какой траектории, с какой скоростью — этого точно никто не знал.
Как раз этими темами занялся Иоганн Кеплер. В 25 лет он написал книгу «Тайна мироздания» о шести известных тогда планетах — в ней он сопоставлял орбиты и «платоновы тела» и искал скрытую математическую гармонию Вселенной. Кеплер был настолько уверен в своей мистической теории, что тут же послал ее крупнейшим астрономам конца XVI века Галилео Галилею и Тихо Браге, и они хотя и отвергли фантазии юноши, но отметили его оригинальность и ум, а Галилей поддержал приверженность молодого ученого гелиоцентрической системе мира. После этого Кеплер вошел в научное сообщество и, осмелев, стал фонтанировать идеями. Одна из них совершенно не понравилась Галилею: молодой коллега утверждал, что Марс движется не по кругу, а по эллипсу. Известие о том, что все орбиты небесных тел — эллипсы, которое нам кажется аксиомой, не сразу было принято астрономами. Неравномерное движение Солнца, Луны и планет тогда объяснялось сложно: считалось, что планета равномерно движется по малому кругу, называемому эпициклом, центр которого, в свою очередь, движется по большому кругу, который называется деферентом.
«Я всегда ценил ум Кеплера — острый и свободный, пожалуй, даже слишком свободный, но способы мышления у нас совсем разные», — отзывался о Кеплере Галилей. А Тихо Браге пригласил молодого астронома к себе, и они десять лет плодотворно работали вместе. Следствием этого сотрудничества как раз и стали знаменитые три закона Кеплера.
Первый закон Кеплера
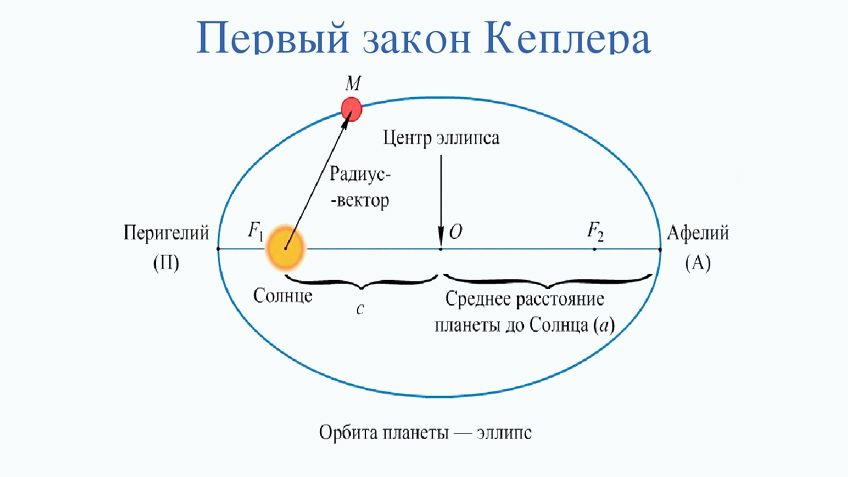
Многолетние наблюдения Браге показали: Марс движется по орбите, но это не окружность. Пытаясь найти объяснения этому загадочному факту, Иоганн Кеплер пришел к первому своему закону: «Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце».
Тут стоит пояснить, что такое фокусы. Эллипс, как вы можете представить, это замкнутая прямая на плоскости. Он симметричен и содержит внутри две оси, проходящие через центр: большую и малую. Оси можно разделить на полуоси, исходящие из центра (это будет радиус орбиты). Если нарисовать на больших полуосях две точки на одинаковом расстоянии от центра, это и будут фокусы. При этом сумма расстояний отрезков от фокусов до любой точки эллипса является постоянной величиной.
Второй закон Кеплера
Второй закон Кеплера определил, как меняется скорость планеты при удалении или приближении к Солнцу. Оказалось, что чем дальше планета находится от Солнца, тем медленнее она движется. А по мере приближения к светилу скорость планеты увеличивается.
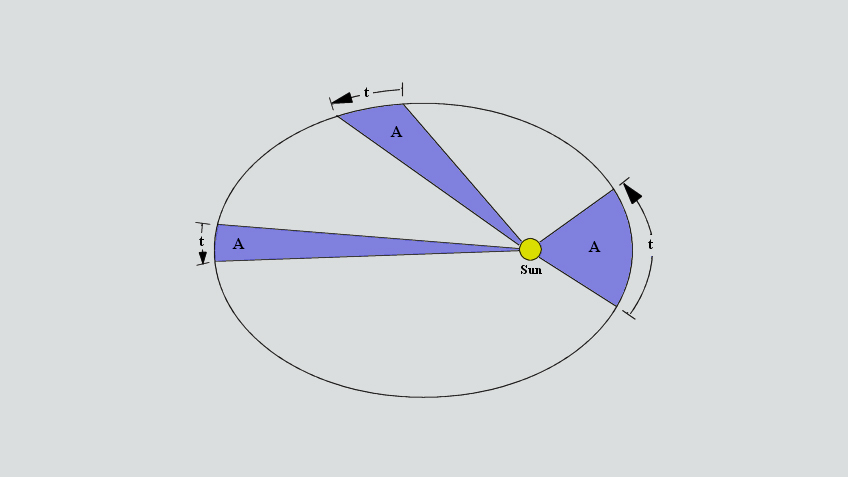
Закон сформулирован так: радиус-вектор, соединяющий планету и Солнце, в равное время описывает равные площади. Радиус-вектор — это линия, соединяющая Солнце и планету, движущуюся по орбите. Проще понять этот закон с помощью наглядной схемы: закрашенные площади равны и проходятся за одинаковое время.
Третий закон Кеплера
Третий закон Кеплера позволяет рассчитать скорость планеты и период ее обращения вокруг Солнца. Он гласит: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет.

T1 и T2 — периоды обращения двух планет вокруг Солнца, a1 и a2 — длины больших полуосей их орбит.
Гармония мира
Математическая красота Вселенной, о которой мечтал ученый, нашла неожиданное подтверждение: выяснилось, что соотношение большого и малого радиуса планет у всех планет Солнечной системы одинаково и совпадает с числом золотого сечения, погрешность составляет доли процента.
«Я выяснил, что все небесные движения, как в их целом, так и во всех отдельных случаях, проникнуты общей гармонией, правда, не той, которой я предполагал, но еще более совершенной», — писал о своих озарениях Кеплер. После его открытий представление о Земле как о центре Вселенной окончательно ушло из астрономии.
Несмотря на столь мощный вклад Иоганна Кеплера в развитие науки, его мать чуть было не сожгли на костре: в 1615 году она была обвинена в колдовстве, посажена на железную цепь в городских воротах и пять лет ожидала казни. Кеплеру пришлось лично защищать ее в суде, забросив астрономию, чтобы опровергнуть полсотни обвинений, в том числе связи с дьяволом, богохульство, порчу, некромантию и т. д. Мать удалось оправдать, но через полгода она умерла — в 1621 году. Кеплер прожил еще девять лет, успев выпустить свою завершающую книгу — «Гармония мира».
Вклад Кеплера в науку высоко оценил Альберт Эйнштейн. «Он жил в эпоху, когда еще не было уверенности в существовании некоторой общей закономерности для всех явлений природы, — писал автор теории относительности. — Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения! Сейчас, когда эти законы уже установлены, трудно себе представить, сколько изобретательности, воображения и неустанного, упорного труда потребовалось, чтобы установить эти законы и со столь огромной точностью выразить их».





























